Sürprizli Su Oyunu: Sürahiler ve Geometriyle Hedefe Ulaşmak!

Zeka oyunlarına meraklı mısınız? Cevabınız evetse, eminim ki “su getirme bulmacası”na denk gelmişsinizdir. Hani şu, farklı boyutlardaki sürahileri kullanarak belirli bir miktarda suyu elde etmeye çalıştığımız klasik problem. Genellikle deneme yanılma yoluyla çözmeye çalıştığımız bu bulmaca, aslında şaşırtıcı bir şekilde geometriyle de çözülebiliyor!

Su Getirme Bulmacasıyla Tanışalım

Belki de aşinasınızdır ama kısaca hatırlayalım: Elimizde iki tane sürahi var, örneğin biri 7 litrelik, diğeri 3 litrelik. Bir de kuyumuz var, yani sınırsız su kaynağımız. Amacımız, bu sürahileri kullanarak tam olarak 5 litre suyu elde etmek. İlk başta biraz kafa karıştırıcı gelebilir, değil mi?

Çoğumuz bu tür bulmacaları sürahileri doldurup boşaltarak, sezgisel bir şekilde çözmeye çalışırız. Bu yöntemle sonuca ulaşmak mümkün olsa da, bazen çok fazla deneme yapmamız gerekebilir. Peki ya bu işi daha sistematik, hatta görsel bir yolla yapabilseydik?

Geometri Sahneye Çıkıyor!

İşte tam bu noktada matematik devreye giriyor. 1948 yılında H.D. Grossman adlı bir matematikçi, bu klasik bulmacayı çözmek için oldukça yaratıcı bir geometrik yaklaşım sunmuş. İlk duyduğunuzda biraz garip gelebilir, ama okuyunca mantığını anlayacaksınız.

Nasıl Çalışıyor? Adım Adım Anlatalım:

Grossman’ın yöntemi, bir grafik üzerinde çizim yapmaya dayanıyor. Şöyle düşünelim:

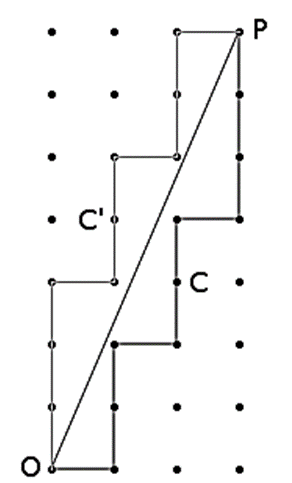
1. Bir Grafik Oluşturuyoruz: Hayali bir grafik çiziyoruz. Yatay eksen küçük sürahinin (3 litre), dikey eksen ise büyük sürahinin (7 litre) kapasitesini temsil ediyor. Başlangıç noktamız (0,0) her iki sürahinin de boş olduğu durumu gösteriyor.
2. Ana Çizgiyi Belirliyoruz: Grafikte (0,0) noktasından başlayıp, küçük sürahinin kapasitesi kadar sağa (3 birim) ve büyük sürahinin kapasitesi kadar yukarı (7 birim) giderek bir nokta işaretliyoruz. Bu noktayı başlangıç noktamızla birleştiriyoruz. İşte ana çizgimiz hazır!
3. Zikzak Çizgisiyle Yolu Buluyoruz: Şimdi bu ana çizginin sağına, yine grafik üzerindeki noktalardan geçen ve ana çizgiye en yakın duran bir zikzak çizgi çiziyoruz. İşte sihir burada başlıyor! Bu zikzak çizgisindeki her bir yatay hareket, büyük sürahiyi doldurup küçük sürahiye boşaltmayı, her bir dikey hareket ise küçük sürahiyi büyük sürahiden doldurup boşaltmayı temsil ediyor.
4. Hedefe Ulaşmak: Bu zikzak çizgisindeki yatay mesafeler, elde edebileceğimiz farklı su miktarlarını gösteriyor. Bizim hedefimiz 5 litre olduğu için, zikzak çizgisinde ana çizgiden yatay olarak 5 birim uzaklıkta olan noktayı buluyoruz.
5. Adımları Çözüyoruz: Şimdi bu noktaya ulaşmak için zikzak çizgisi üzerinde başlangıç noktasından itibaren hangi yolu izlememiz gerektiğine bakıyoruz. Bu yol bize, sürahileri nasıl doldurup boşaltmamız gerektiğini adım adım gösteriyor.

Örneğe Dönelim: 7 ve 3 Litrelik Sürahilerle 5 Litre Su

Metinde verilen örneği bu yöntemle takip edelim:

• 7 litrelik sürahiyi doldurun. (Grafikte yukarı doğru hareket)
• 3 litrelik sürahiyi 7 litrelik sürahiden iki kez doldurun ve her seferinde boşaltın. (Önce sağa, sonra aşağı, sonra tekrar sağa hareket) Bu işlem sonunda 7 litrelik sürahide 1 litre su kalır.
• Kalan 1 litreyi 3 litrelik sürahiye dökün ve 7 litrelik sürahiyi tekrar doldurun. (Aşağı, sonra yukarı hareket)
• 3 litrelik sürahinin kalan 2 litresini 7 litrelik sürahiden doldurun ve 3 litrelik sürahiyi boşaltın. (Sağa, sonra aşağı hareket) İşte hedefimize ulaştık! 7 litrelik sürahide tam olarak 5 litre suyumuz var.

Bu Yöntem Neden İlginç?

Bu geometrik yaklaşım, su getirme bulmacasına farklı bir perspektif sunuyor. Sadece deneme yanılma yerine, görsel bir model kullanarak çözüme ulaşmamızı sağlıyor. Ayrıca, bu yöntemin matematiksel bir temeli olduğunu da görmüş oluyoruz.

İki Çözüm Her Zaman Vardır

Metinde belirtildiği gibi, bu bulmacanın genellikle iki farklı çözümü vardır. Diğer çözümü bulmak için de aynı mantığı kullanarak, ana çizginin sol tarafına bir zikzak çizgi çizebilirsiniz. Bu da size farklı bir dizi sürahi doldurma ve boşaltma adımı sunacaktır.

Sonuç Olarak

Su getirme bulmacası, basit gibi görünse de matematiksel düşünme becerilerimizi geliştirmek için harika bir araç. Grossman’ın geometrik çözümü ise, matematiğin sadece sayılardan ibaret olmadığını, aynı zamanda görsel ve yaratıcı çözümler de sunabileceğini gösteren güzel bir örnek. Bir dahaki sefere bu tür bir bulmacayla karşılaştığınızda, belki de kalemi kağıdı elinize alıp geometrik bir çözüm aramayı deneyebilirsiniz. Kim bilir, belki de matematiğin eğlenceli dünyasında yeni bir keşif yaparsınız!

Siz Ne Düşünüyorsunuz?

Bu geometrik çözüm hakkında ne düşünüyorsunuz? Daha önce bu yöntemi duymuş muydunuz?